Site menu:

ESB, IIT Madras

Research

Currently, I and my students are working on delta-sigma data converters, nyquist rate data converters, continuous-time filters, RF circuits, and phase locked loops. A common focus to all these areas is the reduction of power dissipation. I am also interested in the pedagogy of circuit design. More details of these activities can be seen from our group's research and publications pages. In the past, during my stay in the industry, I have worked on high speed analog to digital converters, high speed serial links, and adaptive equalization. During my PhD, I worked on large dynamic range analog filters using companding techniques.

Delta-Sigma ADCs

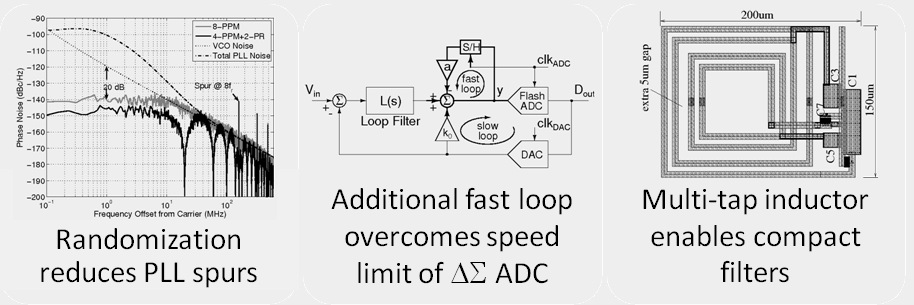
Delta-Sigma ADCs are an attractive alternative to conventional nyquist rate ADCs because they are less reliant on component matching. They require oversampling compared to the nyquist rate for a given bandwidth. Continuous-time Delta-Sigma ADCs operate at a higher maximum speed and consume a smaller power than their discrete-time counterparts. Our work has resulted in a technique for extending the speed limit of Delta-Sigma ADCs in a given process technology. This enables Delta-Sigma ADCs to achieve higher signal bandwidths. We have also worked on the design of a very low power audio Delta-Sigma ADC which has one of the lowest ever reported energy consumption per resolved level, and a technique for using delta-sigma ADCs for sample-by-sample analog to digital conversion without resetting the modulator. The papers describe these ADCs.

Ultra-low-distortion amplifiers and filters

Amplifiers and filters with distortion < -100dBc require special circuit techniques including maximizing loop gain without compromising stability, reducing the current driven from the first stage of the opamp, reducing the inherent distortion of the output stage of the opamp, and cancelling distortion due to passive elements.

Estimation of distortion from individual circuit elements

It is easy to simulate the total distortion of a circuit in circuit simulators, but much harder to tell how much distortion is contributed by individual elements. Our technique to determine per-element distortion contributions, described in the paper below, does not require the designer to know the nonlinear models and does not oversimplify the circuit.

Oscillators and phase locked loops

1/f3 phase noise in quadrature oscillators can be minimized by modifying the impulse sensitivity function. Wide tuning range millimeter wave VCOs can be realized using multiple modes with different effective inductances. Randomizing the positions of charge pump current pulses in a PLL breaks their periodicity and redistributes the reference spurs into broadband noise. The paper below describes the analysis of such pulse position modulated signals and simulated results of spur reduction techniques in wideband PLLs.

Continuous-time filters

Long true-time-delays can be realized over wide bandwidths using reflectios from singly-terminated ladder filters. Low-distortion active filters can be realized using current- efficient feedforward-compensated operational amplifiers in the integrators and feedforward current injection in the summing amplifier which typically operates with a smaller feedback fraction. Passive LC ladder lowpass filters can be made compact using a single inductor with multiple taps. The papers below describe these efforts.

Circuits and systems pedagogy

The papers below discuss alternative approaches to introducing negative feedback circuits such as opamps and phase locked loops.

Companding filters

In conventional linear analog filters, all the internal signal swings are directly proportional to the input signal. In order to meet a given S/N requirement, the noise floor has to be below the smallest signal by the specified amount. Since the maximum possible signal is determined by the power supply, the small signal condition in a conventional filter represents an inefficient usage of the available swing, and gets worse as the dynamic range of the input signals to be handled increases. A better way would be to maintain the internal swings sufficiently above the noise level for all signal levels which necessarily implies a nonlinear processing at the input and the output. i.e. a small signal can be amplified before being fed to the filter so that all the internal swings are still near the maximum, whereas a large signal is fed straight in (sorta like changing gears in a car to change the speed without letting the engine go too slow to sustain ignition or too fast to stay in one piece). Companding is used for the same reason in telephone transmission systems, by using a compressing non-linearity on the transmit side and an expanding non-linearity on the receive side. The situation is a little more tricky with filters because of the presence of elements with memory. If it is done right, companding ought to increase the dynamic range of filters without using extra power, which would not be possible in a "normal" linear filter because larger power is required either to lower the noise floor or to increase the maximum signal swing that can be handled.

Dissertation: Large Dynamic Range Dynamically Biased Log-Domain Filters

This dissertation investigates the enhancement of the dynamic range per unit power consumption of analog filters using dynamic biasing. A technique for realizing dynamically biased log-domain filters while maintaining input-output linearity is presented. This method is much simpler than previously known techniques for realizing large dynamic range filters using syllabic or instantaneous companding. The consequent advantages of the proposed technique are pointed out.

In order to demonstrate the capabilities of the proposed dynamically-biased log-domain filters, a third-order Butterworth filter with a cutoff frequency of 1MHz is designed in a 0.25µm BiCMOS technology. Circuit techniques to ensure proper operation of the filter over a wide range of input currents are presented. With suitable dynamic biasing, the fabricated filter can maintain a THD < 40dB and S/N > 53.7dB for differential input current amplitudes ranging from 3µA to 2.5mA(a range of 58.4dB). In terms of the range of signals that can be handled, the performance is equivalent to that of a conventional filter with a maximum signal to noise ratio of 112dB. The filter draws 575µW from a 2.5V supply in the quiescent condition and 26.1mW with the maximum input amplitude of 2.5mA. The maximum power consumption normalized to the order, the dynamic range, and the bandwidth is 5.9 x 10-20 J, which represents more than an order of magnitude of improvement over existing filters.

The design of a current mode peak detector that can provide the dynamic bias to the filter based on the input signal strength is presented. Satisfactory operation of the peak detector over a range of current amplitudes from 1.4uA to 2.8mA is verified experimentally. The envelope detector in a 0.25µm BiCMOS technology occupies 0.12mm2 and consumes 162.5µW in the quiescent condition. The attack time for a 1:2 increase in the input amplitude is less than 1.2µs and the decay time for a 2:1 decrease in the input amplitude is less than 40µs over the entire range of input amplitudes.

The feasibility of log-domain filtering in standard CMOS processes is verified by an experimental prototype of a 22kHz second-order filter using lateral bipolar transistors and pMOS accumulation capacitors. This filter occupies 0.085mm2 in a 0.25µm CMOS technology, consumes 4.1µW from a 1.5V supply, and has a measured dynamic range of 56.1dB.

The behavior of noise in companding systems is different from that in classical linear systems due to their inherent internal nonlinearity. Methods for analysis and simulation of noise in instantaneous companding processors are presented. Experimental results corroborating the theory are given.