Inverse Imaging & Microwave Remote Sensing
Research in our group is arranged around the following themes which have a good mix of electromagnetics, signal/image processing, numerical linear algebra, and statistics.
Inverse Imaging
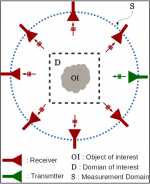 In issues such as breast cancer detection, cancerous tissue have different electrical properties (e.g. dielectric permittivity) as compared to healthy tissue at microwave frequencies. So, if we can acquire an image of the permittivity of breast tissue, we might be able to determine the presence of cancer. In technical terms, we design an experiment (numerical and or physical) where the object of interest is surrounded by transmitters and receivers, and we measure the scattered fields (see figure on the right). We then solve a mathematical problem that takes these fields (input and scattered) and gives us the permittivity as a function of space. But this problem is not very well behaved, so in addition to using electromagnetic solvers, we need clever ideas from linear algebra, image processing, compressive sensing, machine learning, etc. to solve such problems. The benefits? Low-cost, non-invasive, and portable solutions to a very prevalent disease, if the underlying mathematical problem can be solved. The same setup can be generalized to other interesting problems, such as buried object detection, through the wall imaging, etc.
In issues such as breast cancer detection, cancerous tissue have different electrical properties (e.g. dielectric permittivity) as compared to healthy tissue at microwave frequencies. So, if we can acquire an image of the permittivity of breast tissue, we might be able to determine the presence of cancer. In technical terms, we design an experiment (numerical and or physical) where the object of interest is surrounded by transmitters and receivers, and we measure the scattered fields (see figure on the right). We then solve a mathematical problem that takes these fields (input and scattered) and gives us the permittivity as a function of space. But this problem is not very well behaved, so in addition to using electromagnetic solvers, we need clever ideas from linear algebra, image processing, compressive sensing, machine learning, etc. to solve such problems. The benefits? Low-cost, non-invasive, and portable solutions to a very prevalent disease, if the underlying mathematical problem can be solved. The same setup can be generalized to other interesting problems, such as buried object detection, through the wall imaging, etc.
Microwave Remote Sensing
 Various satellite missions have sought to estimate moisture and vegetation content on Earth by making RADAR measurements from space, for e.g. the AirMOSS, SMAP missions by JPL/NASA, or the upcoming NISAR mission of ISRO/JPL. Using electromagnetic scattering tools, we study the interaction of RADAR waves with natural ground objects, in order to understand and interpret the data received. It is known that moisture affects RADAR reflectivity, but many other factors also enter the picture, such as soil roughness, vegetation, etc., and so it is challenging to infer the moisture among other influences. We also apply the same scattering tools for sub-surface studies, particularly for studying sub-surface structures in ice. We primarily use (and develop) finite element based scattering tools in this research because of their versatility and speed. Apart from electromagnetic solvers, we need to apply ideas from statistics and big data to make sense of the large amount of data that is generated in satellite missions.
Various satellite missions have sought to estimate moisture and vegetation content on Earth by making RADAR measurements from space, for e.g. the AirMOSS, SMAP missions by JPL/NASA, or the upcoming NISAR mission of ISRO/JPL. Using electromagnetic scattering tools, we study the interaction of RADAR waves with natural ground objects, in order to understand and interpret the data received. It is known that moisture affects RADAR reflectivity, but many other factors also enter the picture, such as soil roughness, vegetation, etc., and so it is challenging to infer the moisture among other influences. We also apply the same scattering tools for sub-surface studies, particularly for studying sub-surface structures in ice. We primarily use (and develop) finite element based scattering tools in this research because of their versatility and speed. Apart from electromagnetic solvers, we need to apply ideas from statistics and big data to make sense of the large amount of data that is generated in satellite missions.
Faculty
Research Scholars