Metasurfaces

Metasurfaces are planar(2D) metamaterials with subwaveIength thickness. Metasurfaces enable a spatially varying optical response (e.g. scattering amplitude, phase, and polarization), can mold optical wavefronts into shapes that can be designed at will. These structures can be fabricated using Electron Beam Lithography and other nano fabrication processes such as lift-off, RIE etc…

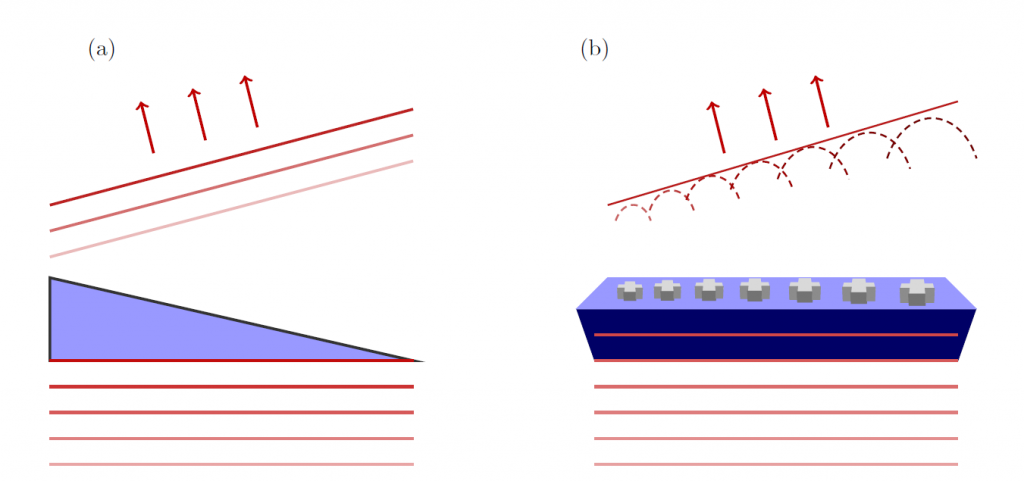
In order to understand how a metasurface operates compared to a ROE or a DOE, a comparison between a refractive prism and its metasurface counterpart is shown in the figure below. A refractive prism has a phase gradient along the interface due to the varying thickness of the glass. This causes the light to refract at the interface and bend according to Snell’s law. On the other hand, a metasurface has an array of meta-atoms on the interface with the same height but different lengths. The phase difference between adjacent neighbours is pi/4 resulting in a phase gradient of 2pi. By choosing an appropriate period and phase gradient, the incident light can be bent in any arbitrary direction.

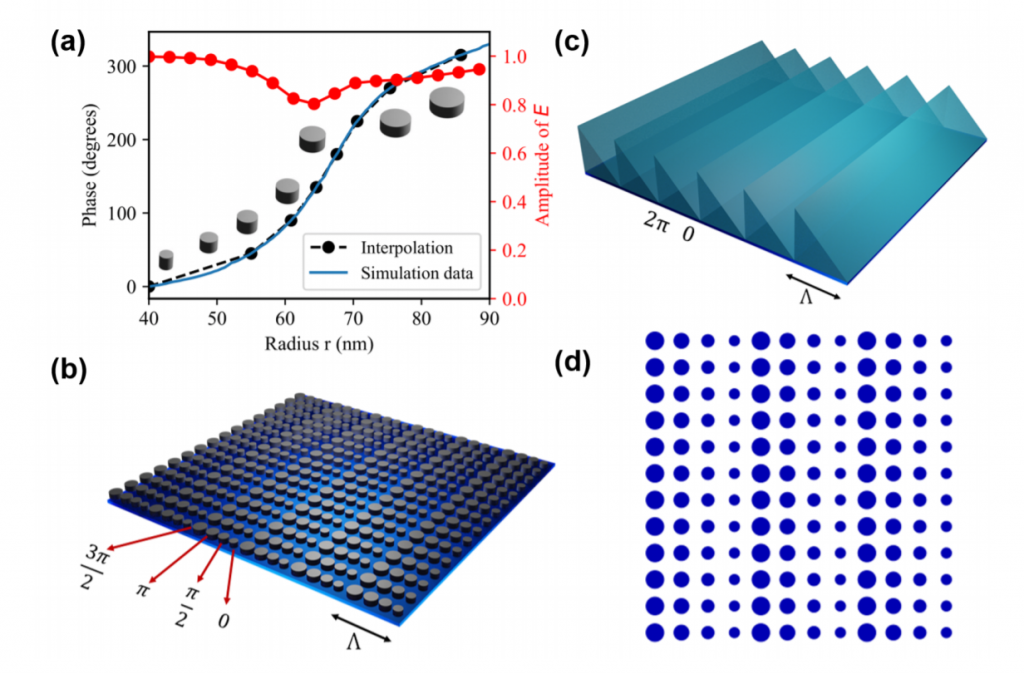
Comparison between a refractive prism and a gradient metasurface (a) Light bending after passing through a refractive prism due to Snell’s law (b) Light bending after passing through a metasurface due to a phase gradient at the interface

In order to physically fabricate a metasurface, we must convert the phase profile of a ROE or a DOE into corresponding metasurface. In this process, the phase profile is quantized into n levels and each pixel is replaced by a meta-atom that shifts the phase of light by the value of the pixel. This process is depicted in the below figure where a blazed grating is converted into a 4-level cylindrical meta-atom metasurface .

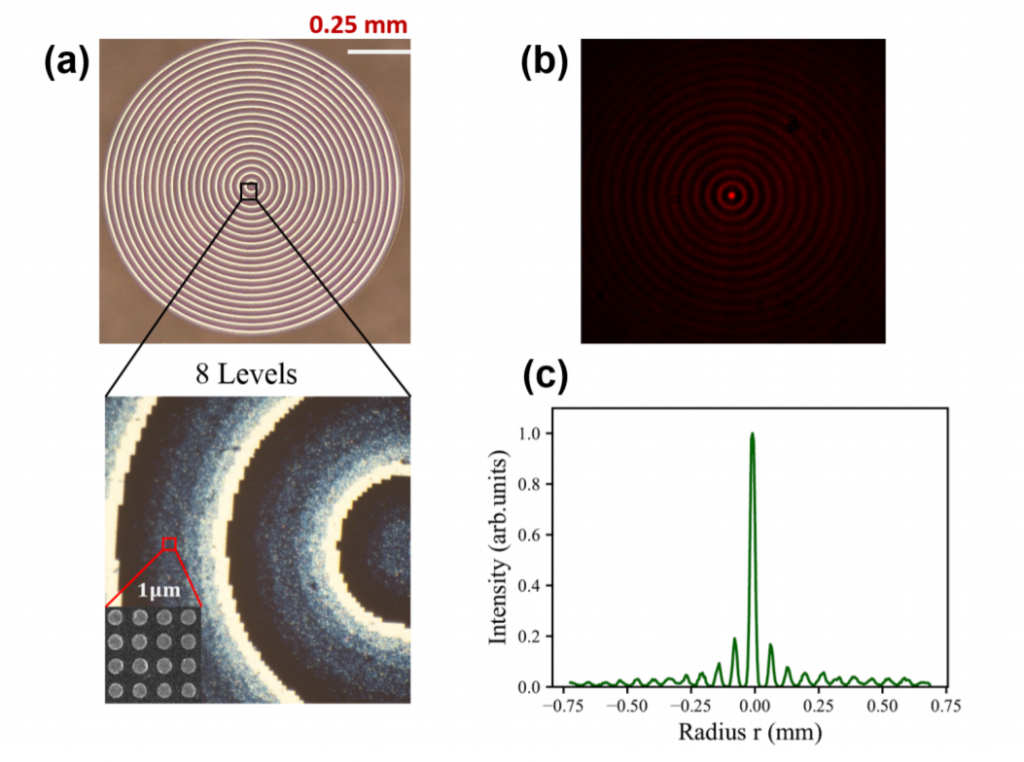
Conversion from a refractive phase profile to a metasurface GDSII layout (a) FDTD lookup data: Transmission amplitude and phase vs variable radius of the cylinder meta-atom at a wavelength of 633 nm (b) 3D phase profile of a blazed grating (c) converted into a 4-phase level metasurface, the cylinder dimensions are fetched from (a), (d) GDSII layout

We have generated LG beams (charge = 3) using a fork hologram. The different fork holograms (for generating LG beams of varying charge) were created by interfering with a spiral phase profile with a plane wave. The resultant phase profiles were uploaded in MetaOptics to generate the desired metasurface layout for fabrication. In order to show the high efficiency of metasurfaces, when compared to binary DOEs, we have designed and fabricated three fork metasurfaces with 2, 4, and 8 levels and the diameter of all the fork gratings is 1 mm.

LG beam generation: Multilevel fork grating metasurfaces and relative efficiency comparison. (a) Microscope images of 2 level, 4 level, and 8 level metasurfaces (b) Zoomedin images highlighting 2, 4, and 8 levels in the metasurfaces (c) Intensity profiles of the LG beams captured using CCD camera and the relative efficiency of generation shown in bar plots (d) Interference with reference beams showing the characteristic fork pattern confirming charge = 3

We generated a Bessel beam using an 8-level meta axicon McLeod (1954). The phase profile of an axicon with cone angle α = 1.5 degrees , and a diameter of 1 mm is generated using the in-built library functions of MetaOptics.

Bessel beam generation: 8 level axicon metasurface characterization (a) Microscope image of fabricated 8 level axicon metasurface (b) Experimentally generated Bessel beam (c) Line intensity profile along the center of (b)

Watch the video lecture on Metasurface by Dr. Raghu

Talk by Raghu Dharmavarapu at the EE Symposium 19 IIT Madras

Tutorial on how to design a metasurface using MetaOptics software