


Next: About this document ...
Up: EC301: Electromagnetic Fields
Previous: Designing a writer for
Subsections
Numerical methods are an indispensable part of today's engineering toolkit. We shall focus
on two popular techniques used to solve electromagnetic problems. (There are many other
approaches and the advanced reader is referred to books like Numerical Techniques in
Electromagnetics, by M. N. O. Sadiku.)
- Finite Difference Time Domain (FDTD) is a popular method used in time varying
problems and solves Maxwell's equations by alternatively solving for the electric and
magnetic fields at each time step.
- Relaxation Method provides an iterative solution to Laplace's or Poisson's equation
in two dimensions. Given the boundary potential, the potential at all lattice points on a
2-D grid is obtained by substituting at each point a weighted average of the values at its
nearest neighbours and repeating the procedure till convergence is achieved.
Most numerical methods will converge to the same solution. However, the final accuracy of
the final result depends on a judicious choice of boundary conditions. The boundary
conditions are themselves not always obvious when one is faced with an engineering
challenge.
Assume a 2-D rectangular cross-section in the y-z plane. The outer
surface of the rectangle is excited by a sinusoidal
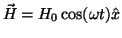 field. We seek the electric and magnetic fields in the interior of the
rectangle. With the magnetic field always perpendicular to the rectangle, the only
components of the electric field will be in the y-z plane. Expanding Maxwell's
equations we get,
field. We seek the electric and magnetic fields in the interior of the
rectangle. With the magnetic field always perpendicular to the rectangle, the only
components of the electric field will be in the y-z plane. Expanding Maxwell's
equations we get,
The time and space derivatives at any location 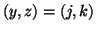 at the time step
at the time step 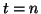 can be further expanded as
can be further expanded as
where 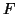 is either the electric or magnetic field component of interest. The equations
for
is either the electric or magnetic field component of interest. The equations
for 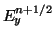 and
and 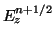 will also include the loss terms
will also include the loss terms 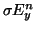 and
and
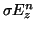 respectively. The implicit FDTD method, which is inherently stable, uses
respectively. The implicit FDTD method, which is inherently stable, uses
![\begin{displaymath}
E^n = \frac{1}{2}\left[E^{n+1/2}+E^{n-1/2}\right]
\end{displaymath}](img100.png) |
(22) |
which upon substitution in (20) will yield an expression suitable for
forward time stepping.
Figure 3:
Positions of the field components using Yee's lattice.
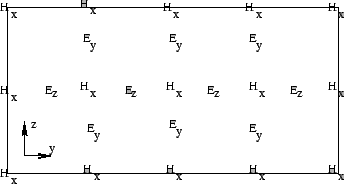 |
An efficient implementation, by Yee, calculates H at 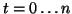 at the integer
locations
(j,k) whereas E is calculated at
at the integer
locations
(j,k) whereas E is calculated at
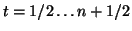 and at half-integer locations
i.e. displaced from the H-nodes by half a cell, as shown in Fig 3. In this
problem, Yee's algorithm would execute as follows
and at half-integer locations
i.e. displaced from the H-nodes by half a cell, as shown in Fig 3. In this
problem, Yee's algorithm would execute as follows
- Start at
 and set E to zero at all interior points.
and set E to zero at all interior points.
- Initialize H on the nodes at the boundary and set to zero elsewhere.
- Calculate
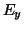 and
and 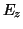 at the half-cell locations at
at the half-cell locations at 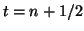 .
.
- Set
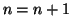 and calculate
and calculate 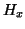 at the nodes.
at the nodes. 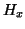 at the boundary is determined
by the sinusoidal excitation
at the boundary is determined
by the sinusoidal excitation 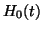 on the boundary.
on the boundary.
- Calculate the nodal average value
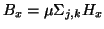 at this time step.
at this time step.
- Check for steady-state or convergence, else go to step 3.
A plot of 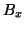 versus
versus 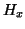 will yield the hysteresis curve for this case.
will yield the hysteresis curve for this case.
Accuracy and stability of the FDTD scheme
Accuracy is often traded-off against speed of computation. Reasonable accuracy is ensured
when the spatial increment
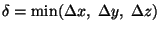 is
one-tenth the wavelength of the excitation. Stability of the FDTD scheme is ensured by
demanding that the time increment satisfy
is
one-tenth the wavelength of the excitation. Stability of the FDTD scheme is ensured by
demanding that the time increment satisfy
![\begin{displaymath}
u_\mathrm{max}\Delta t \leq \left[\frac{1}{\Delta x^2}+\frac{1}{\Delta y^2}+
\frac{1}{\Delta z^2}\right]^{-1/2},
\end{displaymath}](img114.png) |
(23) |
where
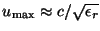 is the maximum phase velocity in the
model.
Assume a uniform grid in two dimensions. The simplest method of estimating
the potential, given boundary conditions, is by replacing the potential at
each point by the average of its neighbours and repeating this process until
the change in the potential at all points becomes arbitrarily small. In
mathematical terms, this would correspond to saying that the potential
is the maximum phase velocity in the
model.
Assume a uniform grid in two dimensions. The simplest method of estimating
the potential, given boundary conditions, is by replacing the potential at
each point by the average of its neighbours and repeating this process until
the change in the potential at all points becomes arbitrarily small. In
mathematical terms, this would correspond to saying that the potential
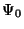 at the origin is
at the origin is
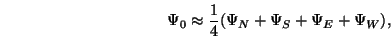 |
(24) |
where the subscripts represent the 4 directions north, south, east and west.
However, this approximation is of 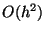 ,
, 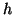 being the distance between
lattice points. A better approximation is obtained by assuming (Jackson 3rd
ed., sec. 1.13)
being the distance between
lattice points. A better approximation is obtained by assuming (Jackson 3rd
ed., sec. 1.13)
A Taylor series expansion of 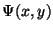 will show that (30) can
be interpreted as
will show that (30) can
be interpreted as
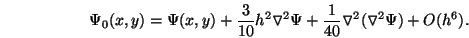 |
(28) |
Iteratively replacing 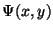 by
by 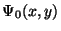 gives us a solution to
Laplace's equation,
gives us a solution to
Laplace's equation,
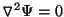 . The added advantage of this
formalism is that we can instead use
. The added advantage of this
formalism is that we can instead use
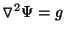 and
find a solution to Poisson's equation with the approximation
and
find a solution to Poisson's equation with the approximation
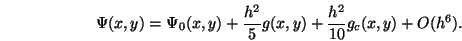 |
(29) |



Next: About this document ...
Up: EC301: Electromagnetic Fields
Previous: Designing a writer for
Anil Prabhakar
2002-09-25
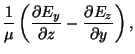
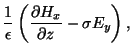
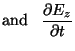
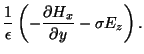
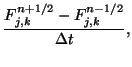
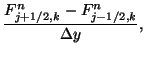
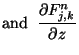
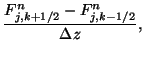
![]() is
one-tenth the wavelength of the excitation. Stability of the FDTD scheme is ensured by
demanding that the time increment satisfy
is
one-tenth the wavelength of the excitation. Stability of the FDTD scheme is ensured by
demanding that the time increment satisfy