Voltage regulator
- Goals:
- Design a voltage regulator for positive voltages
- Understand efficiency and regulation of a regulator
- Appreciate some fine points of small signal “ground”
- Understand how to compensate errors due to opamp input bias currents
- Specifications:
- Vin=9V, Vout=6V unless mentioned otherwise
- 1.2V reference voltage(from a dc source)
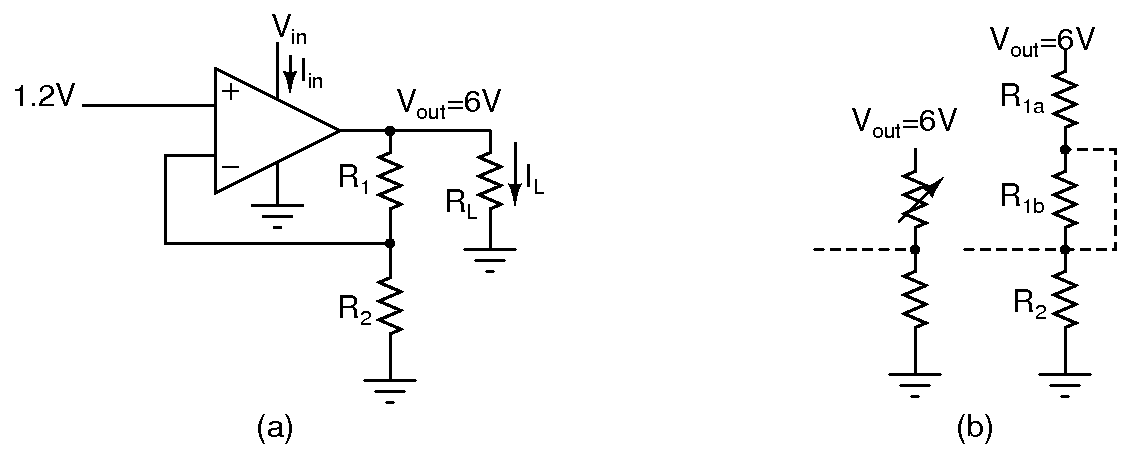
- A voltage regulator is simply a feedback driven voltage controlled voltage source shown above. The input is a temperature stable dc reference(from a bandgap reference, a Zener diode, or a string of forward biased diodes). The feedback resistor can be made variable to have a variable supply such as the one on your bench. In your implementation, realize output voltages of 3V and 6V by shorting out a part of R1 as shown above.
- The amplifier used in the voltage regulator need not be a general purpose opamp. It needs to meet the following criteria:
- The efficiency of a regulator is VoutIout/VinIin. Vout and Vin are given by the specifications. To maximize efficiency, Iout should be close to Iin. i.e. the bias currents in the circuit must be minimized.
- To minimize Vin required to obtain a given Vout, the opamp should have the upper swing limit close to the supply rail. This is achieved by having a single transistor in the common emitter(or common source) configuration-i.e. a single saturation voltage drop-between Vin and Vout. Such a regulator is known as a low dropout regulator, LDO for short(dropout = Vin-Vout).
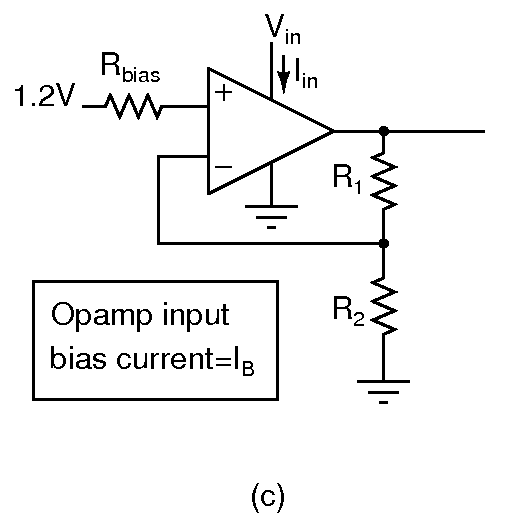
- In your case, the “opamp” will be realized using bipolar transistors. Therefore, transistors in the input differential pair draw a bias current IB. Determine the output voltage in presence of bias currents. How would you overcome this error?
- The above figure shows a scheme for reducing error due to bias currents. What value will you set Rbias to?
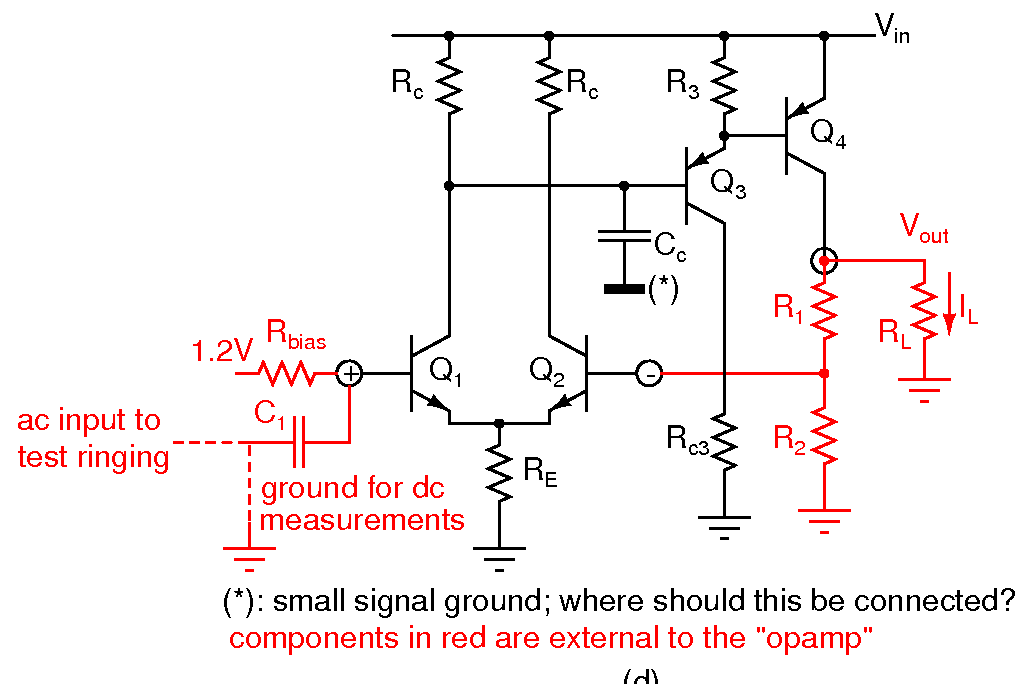
- The above figure shows the complete schematic of the opamp. Cc is a compensation capacitor. In the small signal picture, Cc should be conencted between the base of Q3 and ground. Where should it be connected in the large signal picture? (Hint: think about what happens to the output voltage if there is a jump in the power supply voltage).
- Design the circuit to meet the following requirements. For operating point calculations, you can assume β=∞.
- In no load condition(RL=∞), quiescent currents through Q1,2,3 and the feedback branch R1,R2 are equal
- Quiescent VCE3 should be 2 to 3V.
- Efficiency when RL=125Ω and Vout=6V is 0.96*Vout/Vin.
- Cc should be adjusted as described below.
- Optimizing the dc operating point: Calculate the resistor values to meet the specifications above. If you try to realize these exact values with series parallel combinations of resistors, the assembly can get quite messy. Therefore:
- Use the nearest standard values available. At most, go for a combination of two resistors for each.
- For the feedback network, use five identical resistors, with four in parallel or series as appropriate to realize the ratio accurately
- Ensure that the collector resistances of Q1,2 are identical.
- Build the circuit, compensate it if necessary and measure the dc voltages Vc1,c2 at the collectors of Q1,2.
- If Vc1 is different from Vc2, the differential pair is not perfectly balanced. Q1's collector voltage is fixed by the dc operating point of the following stages. Q2's current needs to be reduced by (Vc1-Vc2)/Rc.
- To do this, measure the voltage VE at the emitter coupled node and adjust RE such that VE/RE,new = VE/RE-(Vc1-Vc2)/Rc.
- Again, use the nearest standard value if possible. Ignore mismatch between Vc1 and Vc2 if it is 100mV or less.
- Wire up the amplifier and apply a small signal square wave riding around 1.2V at the reference input and RL=∞. Does the amplifier settle without ringing? If not, compensate the loop using a capacitor Cc as shown in the figure-connect it to the appropriate small signal ground determined above. Start from small values of Cc and adjust the value to get 5% overshoot. Change RL to 125Ω. Does the ringing get better or worse? Why?
- Test the regulator with load(dc test):
- Determine the output voltages for RL=∞, 2kΩ, 500Ω, 125Ω. The variation in output voltage with the input voltage is known as line regulation.
- Determine the output voltages for Vin=8V, 9V, 10V. Determine the line regulation ΔVout/ΔVin for RL=500Ω.
- Determine the minimum Vin required to get Vout=6V under full load(125Ω).
- What happens if there is a load capacitor CL across RL? Is there a value of CL beyond which the circuit oscillates?
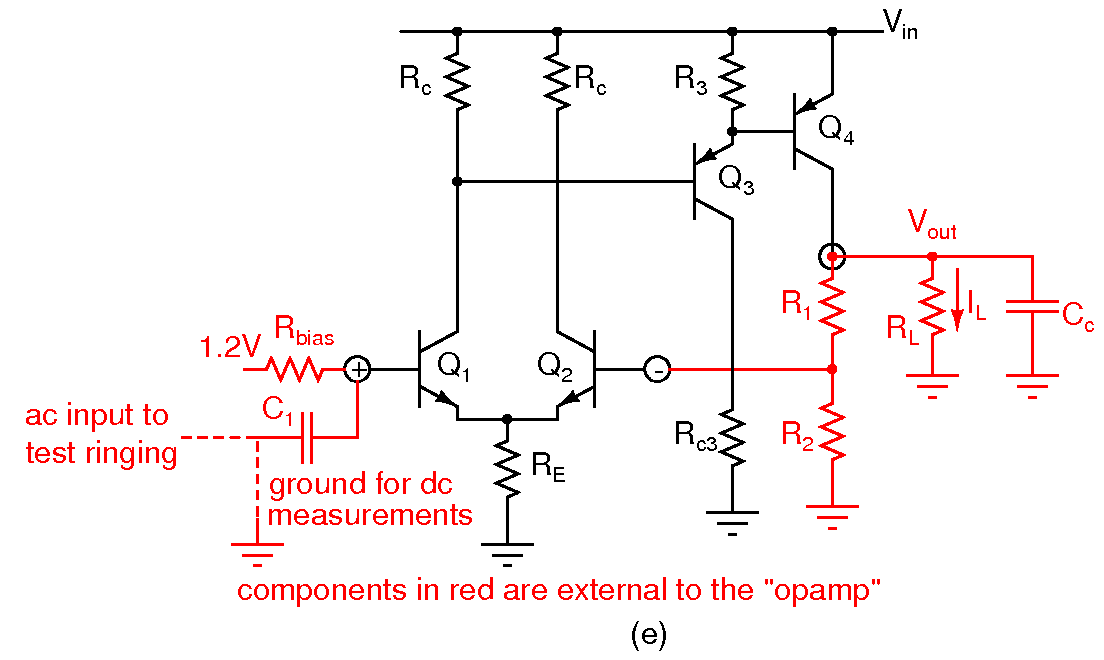
- An alternative method for frequency compensation of the regulator is shown above. What is the required value of the compensation capacitor Cc? Determine the value as before. At which load condition will you do this(RL=∞ or RL=125Ω) to cover all load conditions? LM2940 is compensated in this manner.
- Demonstrate the circuit with a 3V output.
- What is the reason for the relatively poor load regulation? Can you increase the loop gain to improve this? (Hint: bootstrapping may be used to increase the apparent load resistance of the differential amplifier stage).
- Applications: Linear voltage regulators, such as the ones on your bench are made of circuits like this one. They also include the voltage reference generator. The “pass transistor” Q4 is of sufficient rating for the maximum output current(You may be able to see large pass transistors mounted on heatsinks on the backside of some of the power supplies in the lab). Multiple buffer stages may be required(such as Q3) to drive the base current of Q4. Usually the feedback loops have more stages for more gain. For tracking dual power supplies, there is effectively another feedback circuit that looks like an inverting amplifier with the positive Vout as the input. On modern integrated circuits housing entire systems, like large portions of a radio, it is common to find even upto a dozen LDOs powering various blocks. LM2940 is an example of a commercially available LDO. Page 12 of the datasheet has the schematic diagram.
Additional information
The choice of a 1.2V reference is not arbitrary. A temperature stable voltage reference can be realized using bipolar transistors. Its output equals 1.2V(= bandgap of silicon extrapolated to absolute zero). For more information about this, see
- Chapter 11, “Design of CMOS Analog Integrated Circuits”, Behzad Razavi.
- Problem 4 in this assignment of EE539.