Table of Contents
Active RC universal filter
- Goals:
- Understand the operation of an active RC (i.e. opamp-RC) filter
- Use LF347 quad opamp for this experiment
To be done before the lab session
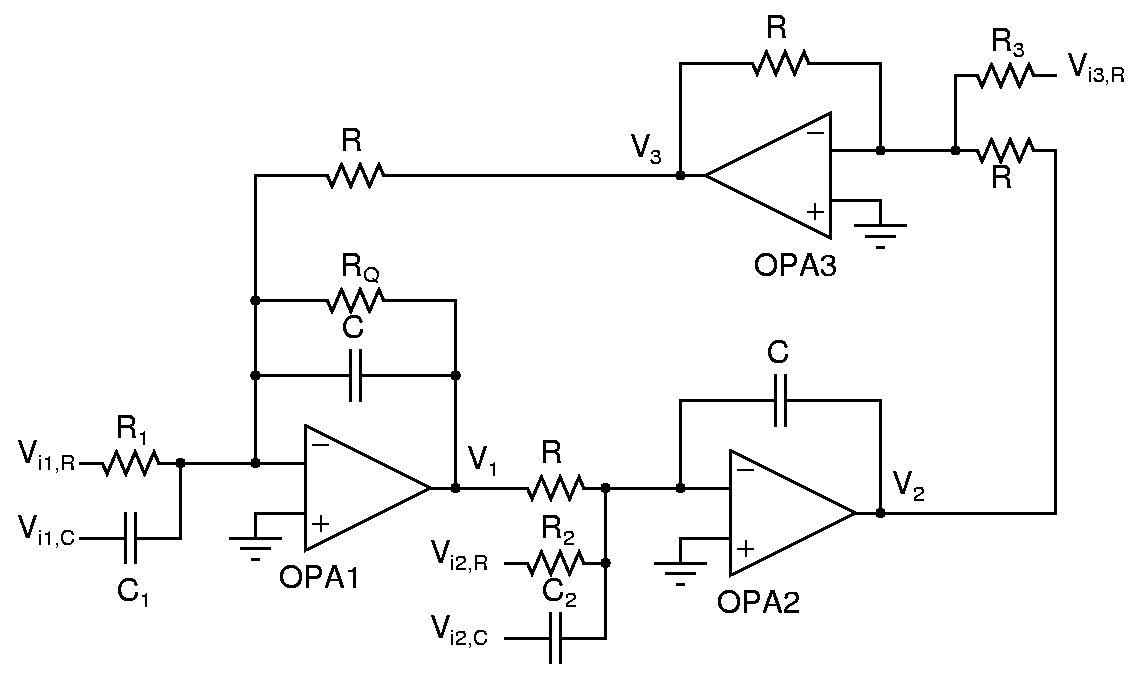
The circuit below can have inputs Vi1,R, Vi1,C, Vi2,R, Vi2,C, Vi3,R and output V1, V2, V3.
Determine the following:
- Transfer functions for all input-output combinations.
- The components on which the resonance frequency and the quality factor depend on.
- The components on which the zeroes depend on.
- Component values for a bandpass filter (with V1 as output) with a resonance frequency of 10kHz and a quality factor of 10. Determine where you will apply the input.
To be done in the lab session
- Build a bandpass filter (with V1 as output) for a resonance frequency of 10kHz and a quality factor of 10. Where will you apply the input? (Omit all unnecessary components from the circuit) Verify its operation.
- While keeping the circuit the same, can you take the output from a different point to realize a lowpass filter? Verify it.
- What are the minimum modifications required to get a notch filter output at V1? Verify it.
- Make the minimum modifications required to obtain a maximally flat lowpass response and verify it. A maximally flat all pole lowpass response has only the highest power of ω in the denominator of |H(jω)|2.
- Modify the above circuit to get a highpass filter output at V1? Verify it.
- Restore the circuit to the bandpass filter in the first part. Replace the opamp LF347 with LM324 which has an identical pin configuration(hopefully you don't have a mess of wires running over the chip!) What do you see? Why?
- Applications: Active RC filters are the most popular topologies of RC filters. For example, they are used as intermediate frequency filters in radio receivers(=radios, mobile phones, GPS, …). At very high frequencies, active RC filters cannot be realized because of difficulties in realizing stable feedback loops with high gains, and gm-C filters are used instead.