Contents

clear
rng(1,'twister');
%close all

Generate a random sym pos def matrix

n = 10;
B = rand(n,n);
%get a random symmetric matrix
B = 0.5*(B + B');
[V,D] = eig(B);
%make its n eigs > 0 by picking from uniform pd [1,n^2]
Dp = randi(n^2,n,1);
A = V * diag(Dp) * V';
%prepare a col vector b for use in the quadratic functional
b = rand(n,1);

Prepare the quadratic functional and sim params

f = @(x) 0.5 * x' * A * x - b' * x;
gradf = @(x) A * x - b;
%get the true soln
x_true = A\b;
%pick a random starting point
x0 = rand(n,1);
%sim params
max_iter = 50;
tol = 1e-6; %how low we want the gradient to be

Solve using gradient descent and exact step size

%x = x - alpha * gf, where alpha = grad(f)' * grad(f)/(grad(f)'*A*grad(f))
x = x0;
x_SD = [x];
gf = gradf(x);
gf_log = [norm(gf)];
%set initialization params
k = 0;

while norm(gf) > tol && k < max_iter
    alpha = gf'*gf/(gf'*A*gf); %step length
    x_new = x + alpha * (-gf); %move
    gf = gradf(x_new); %gradient for next step
    gf_log = [gf_log, norm(gf)];
    x = x_new;
    k = k+1;
    disp(['SD: k=' num2str(k) ', gf=' num2str(norm(gf))]);
    x_SD = [x_SD, x];
end

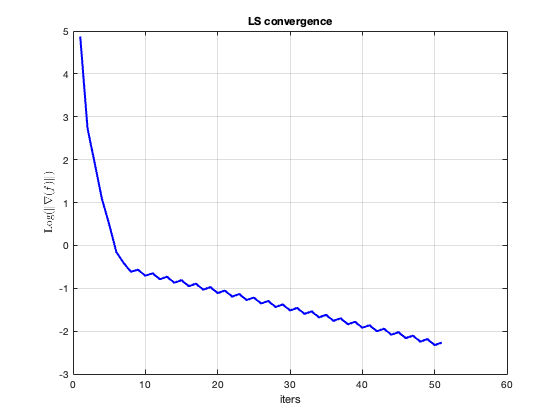
figure;
plot(log(gf_log),'b','LineWidth',2); grid;
xlabel('iters');ylabel('Log($\|\nabla(f)\|$)','Interpreter','latex');title('LS convergence');

SD: k=1, gf=15.5027
SD: k=2, gf=6.7961
SD: k=3, gf=2.9588
SD: k=4, gf=1.6365
SD: k=5, gf=0.85209
SD: k=6, gf=0.66311
SD: k=7, gf=0.54088
SD: k=8, gf=0.5665
SD: k=9, gf=0.49212
SD: k=10, gf=0.52181
SD: k=11, gf=0.4538
SD: k=12, gf=0.48127
SD: k=13, gf=0.41856
SD: k=14, gf=0.44389
SD: k=15, gf=0.38605
SD: k=16, gf=0.40942
SD: k=17, gf=0.35608
SD: k=18, gf=0.37763
SD: k=19, gf=0.32843
SD: k=20, gf=0.3483
SD: k=21, gf=0.30292
SD: k=22, gf=0.32126
SD: k=23, gf=0.2794
SD: k=24, gf=0.29631
SD: k=25, gf=0.2577
SD: k=26, gf=0.2733
SD: k=27, gf=0.23769
SD: k=28, gf=0.25208
SD: k=29, gf=0.21924
SD: k=30, gf=0.2325
SD: k=31, gf=0.20221
SD: k=32, gf=0.21445
SD: k=33, gf=0.18651
SD: k=34, gf=0.1978
SD: k=35, gf=0.17203
SD: k=36, gf=0.18244
SD: k=37, gf=0.15867
SD: k=38, gf=0.16827
SD: k=39, gf=0.14635
SD: k=40, gf=0.1552
SD: k=41, gf=0.13498
SD: k=42, gf=0.14315
SD: k=43, gf=0.1245
SD: k=44, gf=0.13204
SD: k=45, gf=0.11483
SD: k=46, gf=0.12178
SD: k=47, gf=0.10592
SD: k=48, gf=0.11233
SD: k=49, gf=0.097691
SD: k=50, gf=0.1036

Published with MATLAB® R2022a