DataTypeComparison¶
Comparison of the results of simulating OOMMF problem with 'double' and 'float' for different control point specifications¶
THE PROBLEM:
The problem that was taken into contention for simulating had the following specifications:
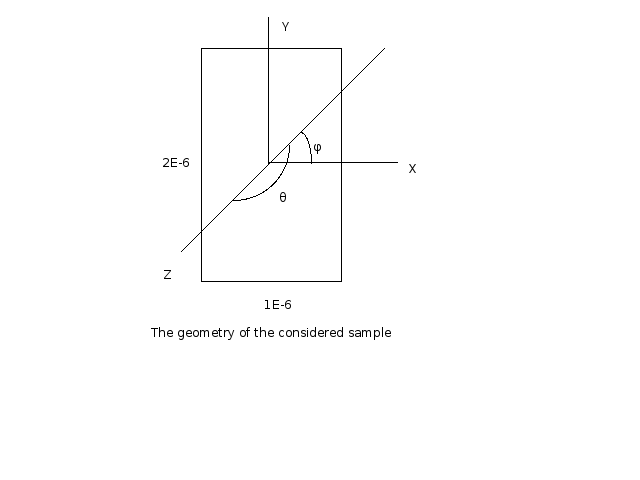
1) The geometry considered was the following:
2) Initial Magnetization: initmag2.ovf
The problem which was simulated for obtaining the initial magnetization for this problem, had the following specifications:
Starting orienation: Q=89°, F=90°
Applied field: Bx=100 mT to 0 mT in steps of 25 mT,200 iterations at each step
Relaxation magnetization at Bx=0 mT, with max torque=10-4
Precision: long double (default setting in 'app/mmsolve/fft.h'
No time control point specification was given.
The OMF file was converted to an OVF file using 'tclsh oommf.tcl avf2ovf <initmag2.omf >initmag2.ovf'(3) Field Range: 0.0 0.0 0.0 0.0 0.0 0.0 1 -torque 1e-5 -time 1e-7
This implies that 0 field was applied and the simulation was ended when either the torque at a step was less than 1E-5 or when the elapsed field time for the current field step reaches 1E-7 seconds.
These specification were changed for the different simulations
Calculation of Metric
The comparison of 2 simulations are done on the basis of their OVF files corresponding to a particular step. The OVF file has the magnetization vector values at all the points considered in the geometry of the sample.
The format of the OVF file can be understood from the following sample OVF file:
The metric which we have considered is the Euclidean Norm which is calculated in the following way:
Let one of the vectors be given by *X*=[x 1, x 2,...x M]
Let the other vector be given by *Y*=[y 1, y 2,...y M]
The Euclidean Norm is given by: [(x 1-y 1) 2+(x 2-y 2) 2+...(X M-y M) 2] 1/2
COMPARISON:
| No. | Data Type | M i (x,y) | m x h | _ Iterations | max( m i - m 0 ) | Time spent simulating | Figure | Comments | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Double | M 0 | 1e-4 | Reference | initmag2.ovf | |
2 | Double | M 1 | 10000 | 1.62e-2 | 398.05 seconds | Figure 1 | The largest error is seen approximately at the coordinates (0.0, 1.0) and (1.0, 1.0), where, from the field plot we can see that,a discontinuity arises. | ||||
| 3 | Float | M 2 | 10000 | 4..5e-3 | 372.54 seconds | Figure 2 |
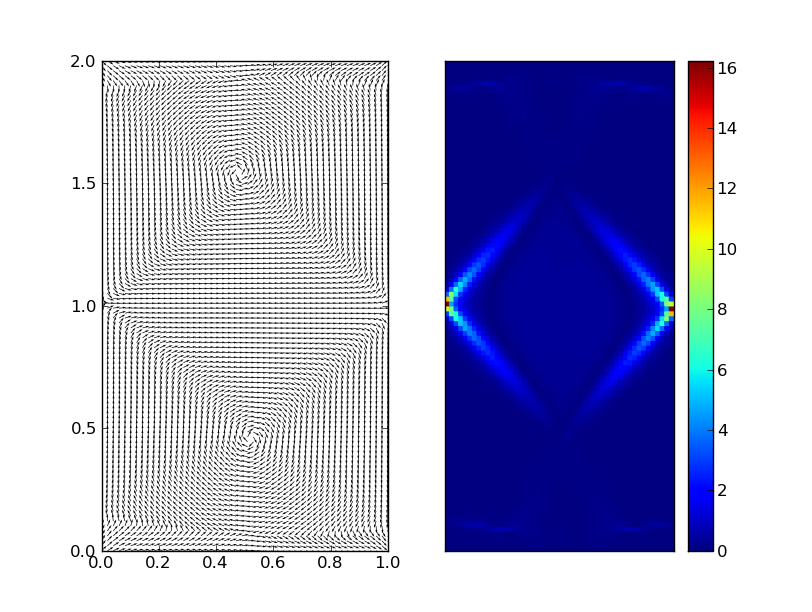
Figure 1: Magnetization and Euclidian Norm after simulating with double
with different time control points
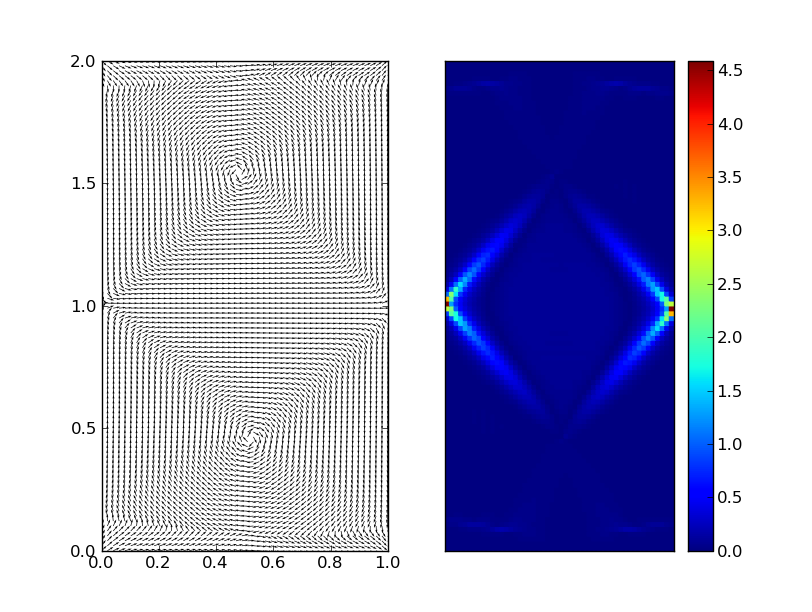
Figure 2: Magnetization and Euclidean norm after simulating with double and float
with same control specifications.
