Data, Statistics and Probability

Lecture 4: Discrete Random Variables

Jul-Nov 2022

Recap

  • Probability space: Sample space , events collection, probability function
    • Sample space: set of all outcomes
    • Events collection: subsets of sample space, includes , closed under union/intersection
    • Probability function: events collection s.t. and
  • Conditional probability
    • (for an event with )
    • Conditional probability space - allows for quick computation of probabilities
  • Independence
    • , are independent events if
    • Stochastic independence might be true even without physical independence

Random variables

Random variables are functions from the sample space to the real line.

Probability space: , events collection,

  • Random variable : function from sending an outcome to
    • Technical: should be in events collection for all
  • Example: Toss a coin
    • (1) , , (2) , , (3) ,
    • Suppose coin lands . What are the values of , , ?
  • Example: Throw a fair die twice, outcome
    • (1) , 'sum of throws', (2) , 'max of throws'

Why random variables?

If outcome is very rich, study parts of it by defining random variables

  • Example: IPL match, Outcome: Entire scorecard of a match (cricsheet.org)
    • Difficult to define probability function for entire outcome
    • A large number of random variables can be defined
      • Runs scored in first ball, Target set, Number of wickets etc.

Distribution function of a random variable

Consider a random variable in a probability space with probability function .

Distribution Function of , , is defined as

  • Distribution function is commonly called Cumulative Distribution Function (CDF)

  • Example: Toss a coin, ,

    • , ,

    • , ,
    • , ,

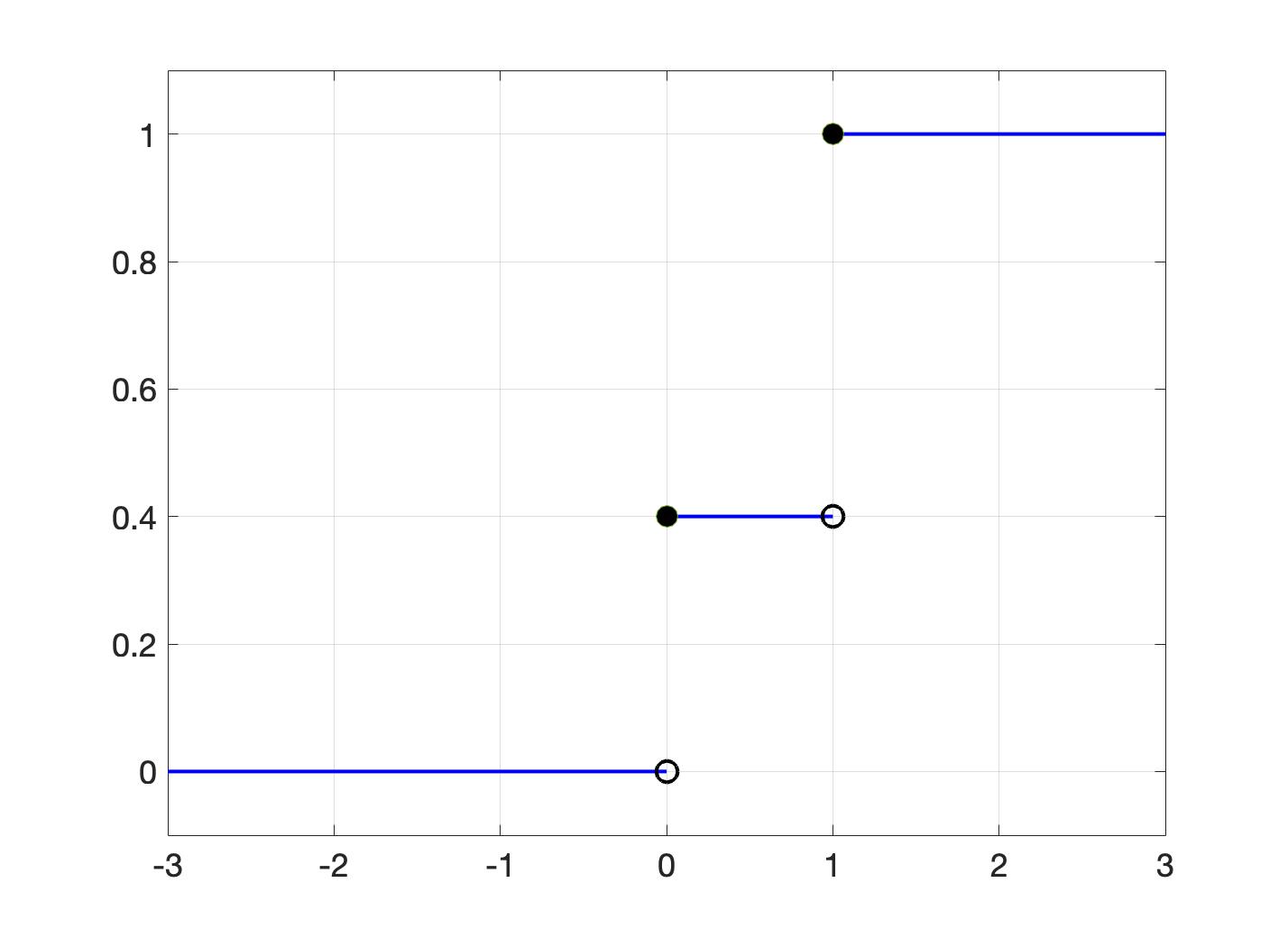
Examples of Distribution Functions

  • Throw a fair die, denotes the throw

  • from some probability space

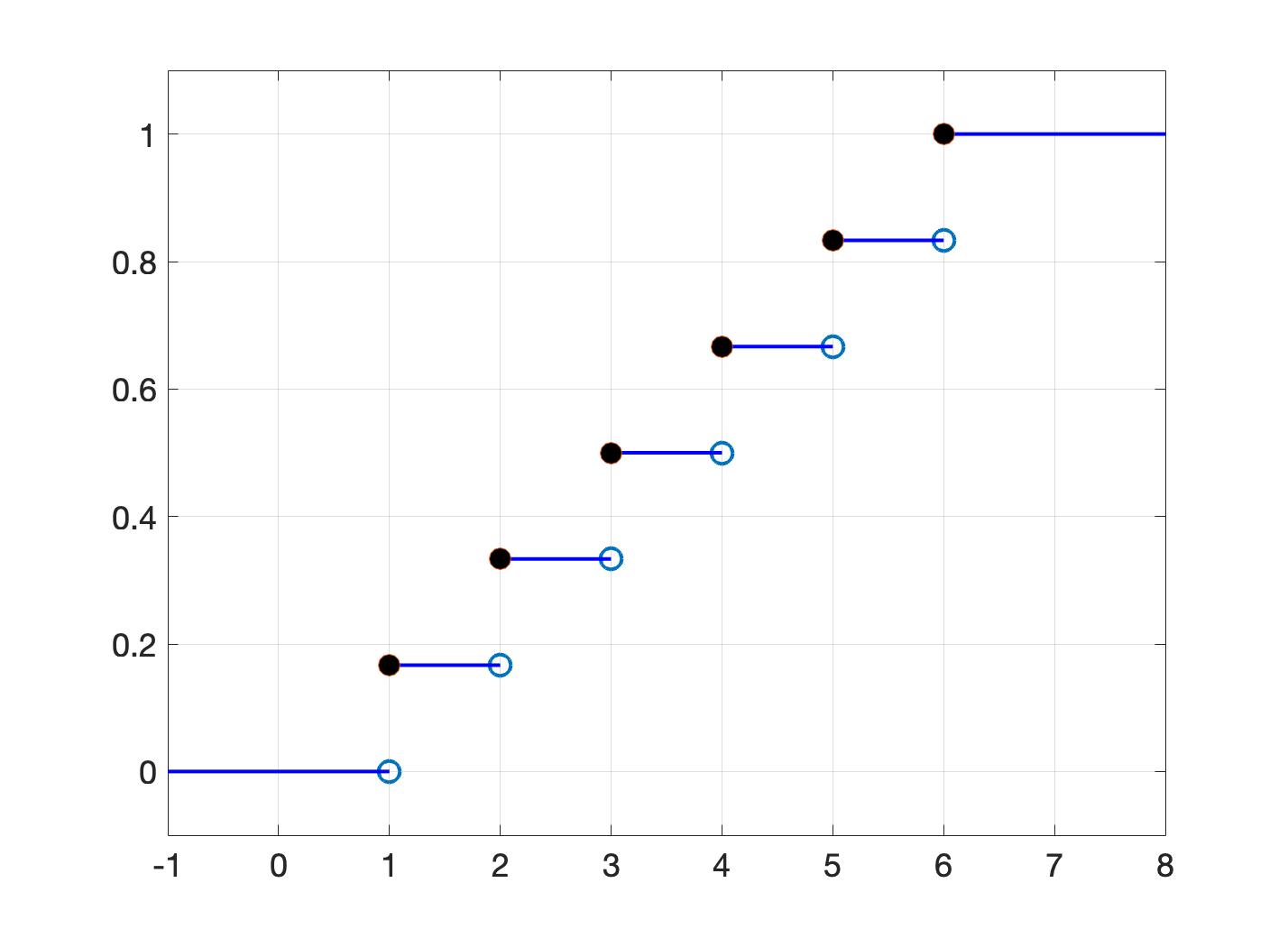
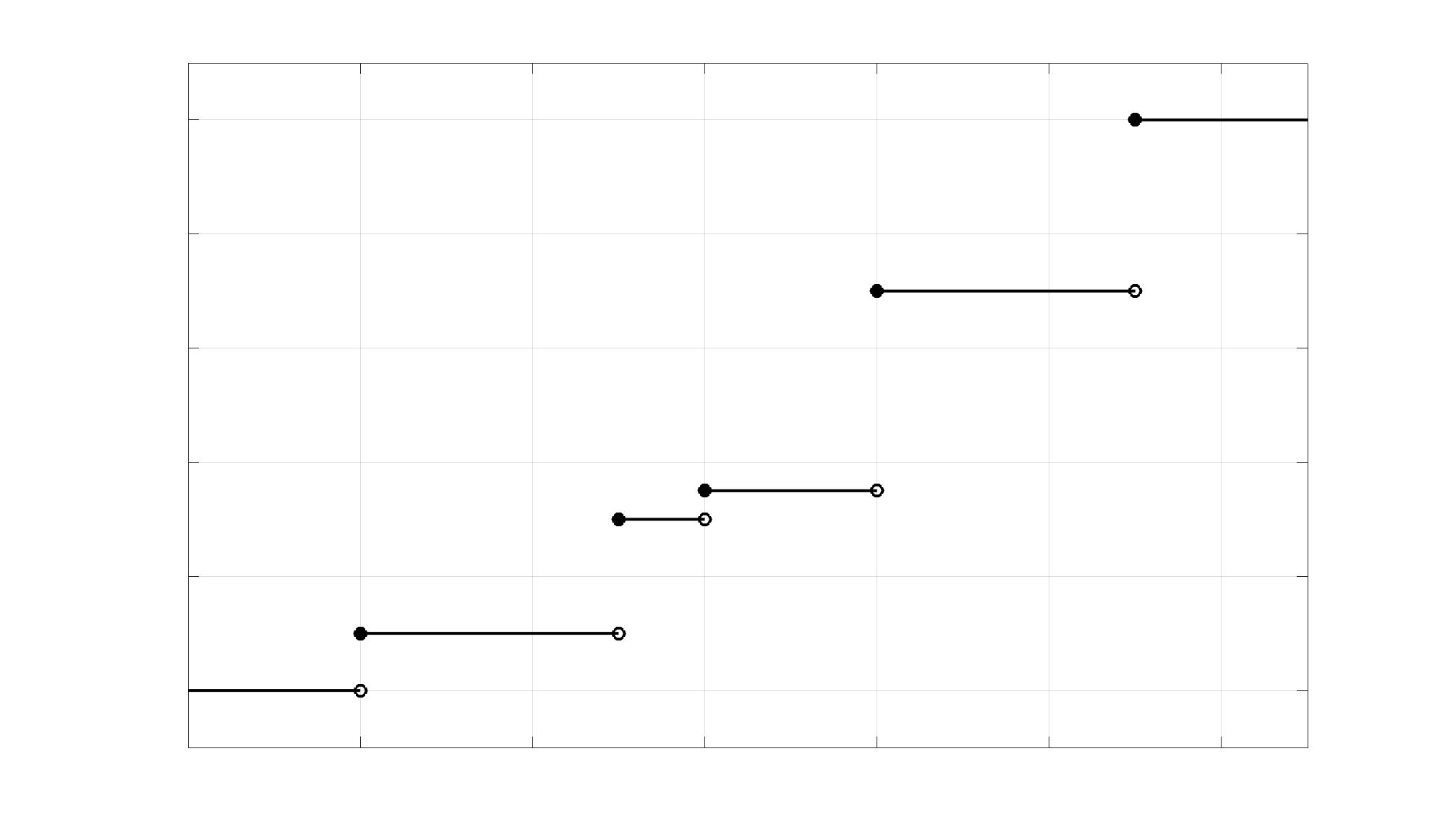
Properties of CDF

  • ,
  • is non-decreasing, i.e. if ,
    • So,
  • Technical: is continuous from the right

Discrete random variables

Discrete random variables take values in a discrete set

  • Range of a random variable , denoted , is the set of values taken by a random variable
  • is discrete if is discrete
  • What is discrete? A partial definition....
    • : non-vanishing minimum distance between any points
      • , etc
    • does not contain any interval
  • If is discrete,

Probability mass function for discrete random variables

Consider a discrete random variable in a probability space with probability function .

Probability Mass Function (PMF) of , , is defined as

  • Example: Toss a coin, ,

    • , ,

    • , ,
    • , ,

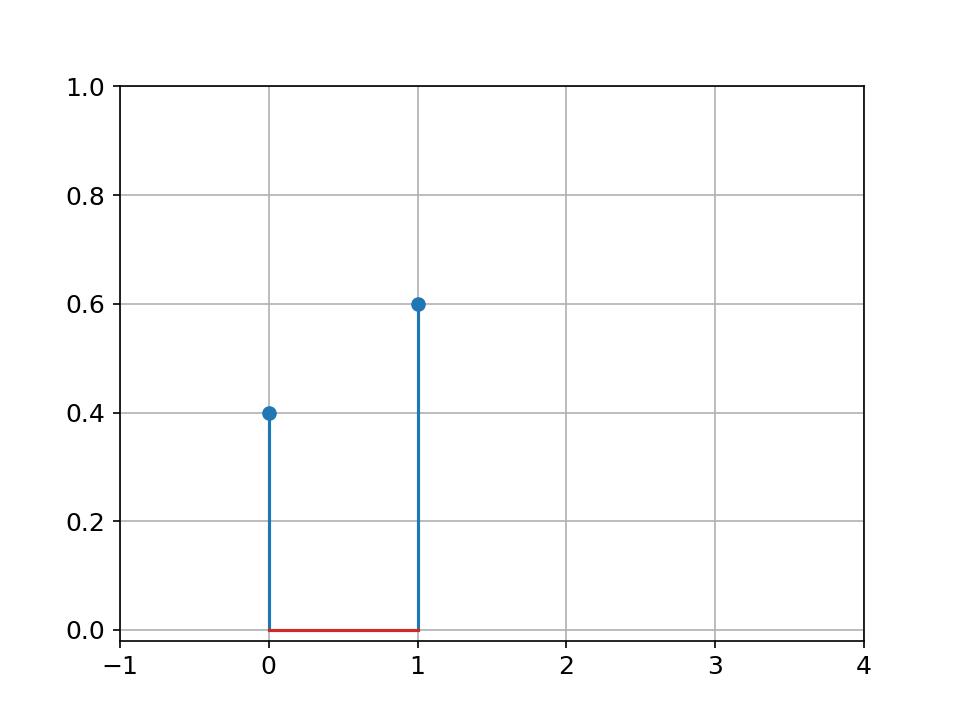
Examples of PMFs

  1. Uniform,
  2. , (called Binomial)

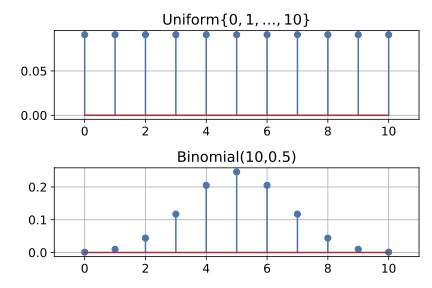
Properties of PMF

: random variable with range

Example: Throw a fair die twice, outcome

    • Step 1:
    • Step 2: For ,
    • Step 1:
    • Step 2: For ,

PMF CDF

  • CDF to PMF
    • Step 1: points of discontinuity, Step 2: length of jump

  • PMF to CDF

Discrete distributions: Bernoulli, Binomial

Some PMFs (or CDFs) occur commonly, and are named for ease of reference

  • Bernoulli, , , PMF ,
    • Indicator random variable of an event , , Bernoulli
  • Binomial, : positive integer, ,
    • PMF: ,
    • Number of 1s in independent Bernoulli, Binomial
      • ,

Binomial: PMF, CDF

PMF: ,

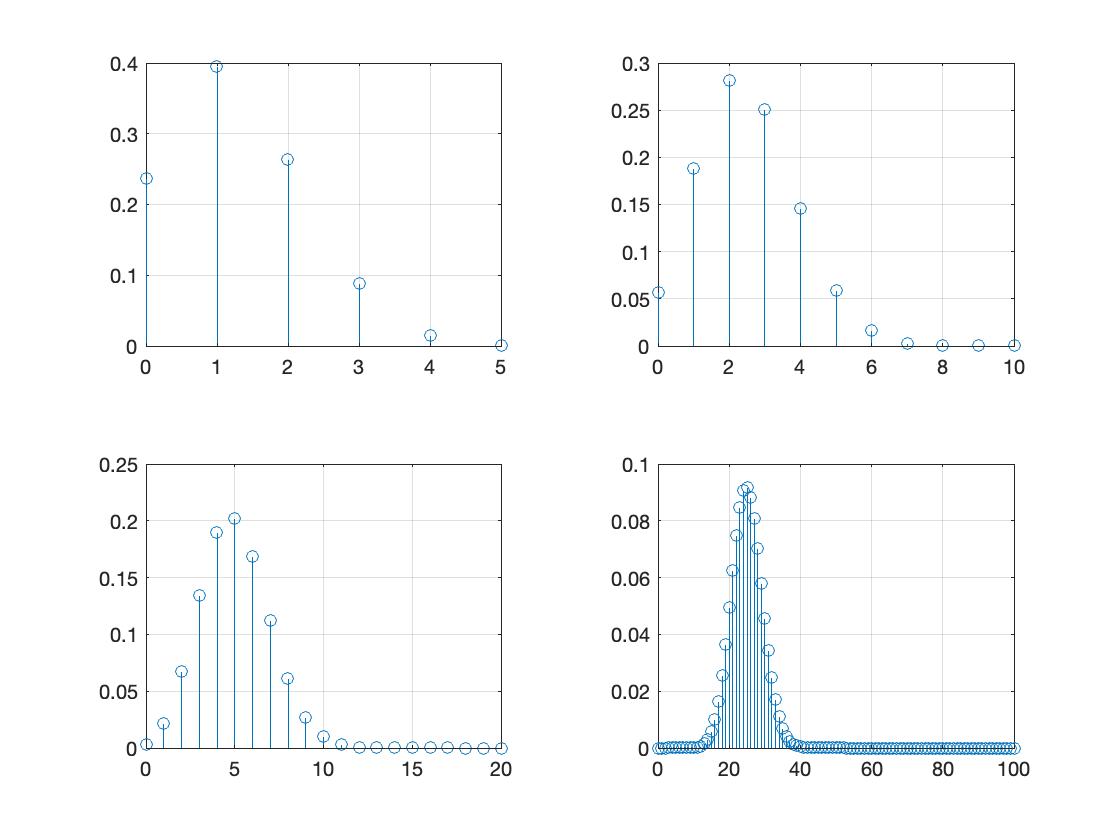
CDF:

Discrete distributions: Geometric, Poisson

  • Geometric, ,
    • PMF: ,
    • number of independent Bernoulli trials till 1 is obtained, Geometric
  • Poisson, ,
    • PMF: ,
    • Binomial, for a fixed
      • and
    • Poisson can be much more convenient that Binomial!

Geometric and Poisson PMFs

Geometric

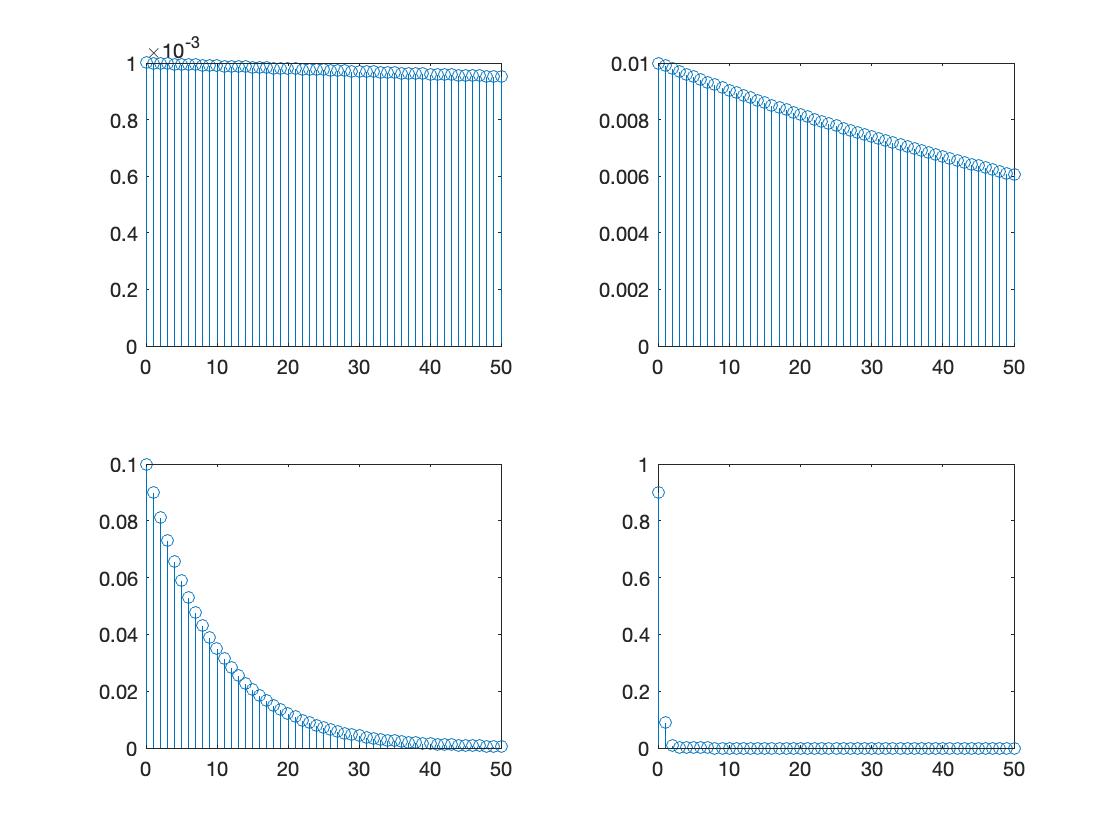
Poisson

Discrete distribution with PMF

Given any valid PMF , suppose that a random variable

  • , which is called support of (or of )

  • What about the probability space needed for defining ?

    • , Events: power set of ,
    • can be defined on the above probability space

  • For many textbook computations, the connection to a probability space is not necessary

    • Quite often, random variables are defined vaguely as "algebraic variables taking random values"

  • In most real-life probabilistic models, random variables are defined in a probability space

    • Computations without understanding the probability space can lead to faulty conclusions