Classification of Operators
Andrew Thangaraj
Aug-Nov 2020
Recap
- Vector space \(V\) over a scalar field \(F= \mathbb{R}\) or \(\mathbb{C}\)
- \(m\times n\) matrix A represents a linear map \(T:F^n\to F^m\)
- dim null \(T+\) dim range \(T=\) dim \(V\)
- Solution to \(Ax=b\) (if it exists): \(u+\) null\((A)\)
- Four fundamental subspaces of a matrix
- Column space, row space, null space, left null space
- Eigenvalue \(\lambda\) and Eigenvector \(v\): \(Tv=\lambda v\)
- There is a basis w.r.t. which a linear map is upper-triangular
- If there is a basis of eigenvectors, linear map is diagonal w.r.t. it
- Inner products, norms, orthogonality and orthonormal basis
- There is an orthonormal basis w.r.t. which a linear map is upper-triangular
- Orthogonal projection: distance from a subspace
- Adjoint of a linear map: \(\langle Tv,w\rangle=\langle v,T^*w\rangle\)
- null \(T=\) \((\)range \(T^*)^{\perp}\)
- Self-adjoint: \(T=T^*\), Normal: \(TT^*=T^*T\)
- Complex/real spectral theorem: \(T\) is normal/self-adjoint \(\leftrightarrow\) orthonormal basis of eigenvectors
- Positive operators: self-adjoint with non-negative eigenvalues
- Isometries: normal with absolute value 1 eigenvalues
Operators and their null/range spaces
\(V\): inner product space, dim \(V=n\), \(T:V\to V\)
| Type | Property |
|---|---|
| Any | dim null \(T\) + dim range \(T = n\) |
| null \(T=\) \((\)range \(T^*)^{\perp}\) | |
| dim range \(T=\) dim range \(T^*\) | |
| Upper-triangular matrix w.r.t. orthonormal basis | |
| Invertible | dim null \(T=0\), dim range \(T=n\) |
| Diagonalizable | No special property |
| Normal | null \(T=\) null \(T^*\), range \(T=\) range \(T^*\) |
| null \(T=\) \((\)range \(T)^{\perp}\) |
Operators and their eigenvalues/eigenvectors
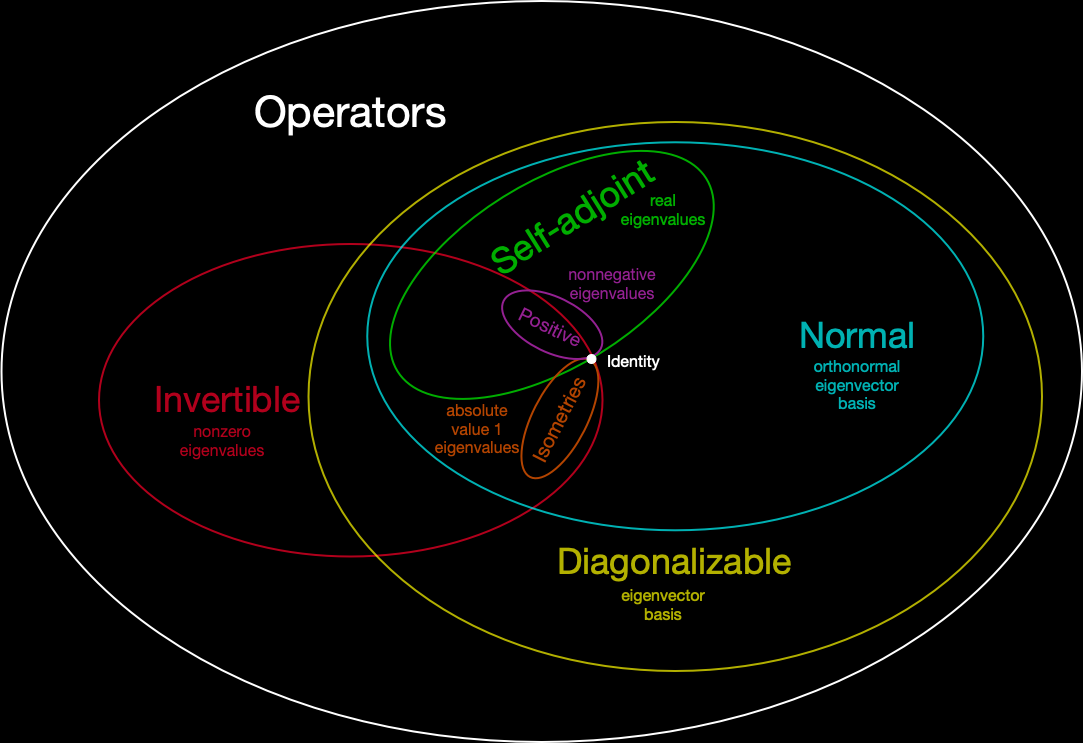
Operators and norms/inner products
(In a complex space) Self-adjoint iff \(\langle Tv,v\rangle\) is real
Normal iff \(\lVert Tv\rVert=\lVert T^*v\rVert\)
Isometry iff \(\langle Tu,Tv\rangle=\langle u,v\rangle\)