Understand how to realize filters using transconductors and capacitors

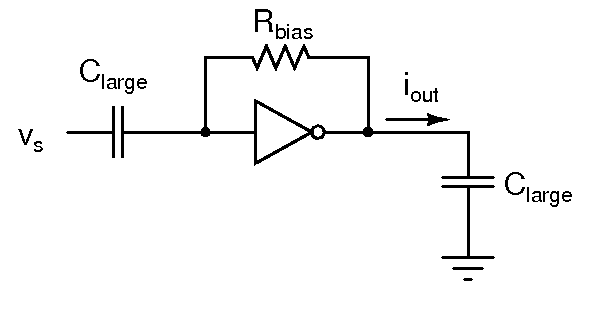
The circuit above shows an inverter self biased using a resistor R_bias. An ac signal v_s is coupled to the input and the output is incrementally shorted for ac signals. What is i_out? What will you do to make i_out/v_s approximately equal to the g_m of the inverter and independent of R_bias?

Use a 6V supply for this experiment

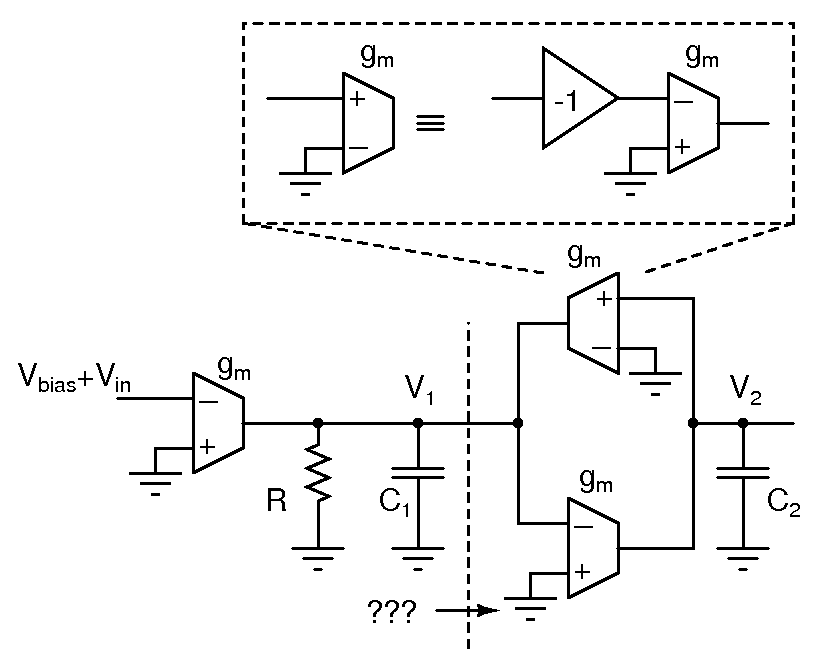
Design the gm-C filter shown above for a resonant frequency of 10kHz and a quality factor of 2. Determine the transfer functions between the input and V₁ and V₂. Build the filter using only transconductors and capacitors. i.e. the resistor R and the positive transconductor +g_m in the filter should be realized using only the inverters available on a 4069. You should arrange the circuit such that the input dc bias is the self bias voltage of the inverter.

Measure the circuit and verify that it realizes the transfer functions given above. Filters can be measured by injecting sinusoidal inputs and observing inputs and outputs on 2 channels of an oscilloscope. Also, the phase difference between input and output can be gauged from X-Y plots, and the center frequency determined. Observe the step response by injecting a low frequency square wave to the filter.

Tune the filter using the power supply voltage and verify that it tunes as expected. The voltage V_bias at the input should track the self bias voltage of the inverter as the power supply is changed.

What is the equivalent of the circuit on the right side of the dashed line in the figure above?

Since inductors are too bulky, filters are frequently made using only capacitors and active elements. One of the techniques is using transconductors and capacitors, such as the one here. This type of filter is used to realize very high frequency active filters. e.g this paper which uses a more complicated transconductor, or this one which uses CMOS inverters.